3) Solve the equation x 2 25 = 0 Solution x 2 25 = (x 5)(x 5) => we have to solve the following 2 equations x 5 = 0 or x 5 = 0 so the equation have two decisions x = 5 and x = 5 Related Resources Polynomial identities quiz Simplifying polynomial expressionsSolution 1 y = 3x 5 is a linear equation in two variables and it has infinite solutions As for every value of x there will be a value of y satisfying above equation and vice versa Hence, the correct answer is (iii) Solution 2 (i) 2x y = 7 For x = 0 2 (0) y = 7 y = 7 Algebraic Formulas For Class 9 th (ab) 2 = a 2 2abb 2 (a−b) 2 = a 2 −2abb 2 (ab)(a–b) = a 2 –b 2 (xa)(xb) = x 2 (ab)xab (xa)(x–b) = x 2 (a–b)x–ab (x–a)(xb) = x 2 (b–a)x–ab (x–a)(x–b) = x 2 –(ab)xab (ab) 3 =a 3 b 3 3ab(ab) (a–b) 3 = a 3 –b 3 –3ab(a–b) (xyz) 2 = x 2 y 2 z 2 2xy2yz2xz (xy–z) 2 = x 2 y 2 z 2 2xy–2yz–2xz

Which Of The Pairs Of Linear Equations Has Unique Solution No Solution
(x-y)^3 formula class 9
(x-y)^3 formula class 9-=−9 3 By division we get =−3 x 4 2 y 1 3 Now draw a graph using the points (4, 1) and (2, 3) Join the points through a line and find the value of y (i) Based on the graph, Consider x = 4 on Xaxis Now the line joining the two points and a point on the Yaxis gives the value of y Therefore, when x = 4 the value of y = 1Important Maths Formulas for Class 9 1 Polynomial Expresssions Formulas Monomial 3, 2x, 2 3y etc 3, 2 x, 2 3 y e t c Binomial (2x 3y), (3x −2y) etc ( 2 x 3 y), ( 3 x − 2 y) e t c Trinomial x2 4x5 etc x 2 4 x 5 e t c



1
Steps for Solving Linear Equation y=3x9 y = 3 x 9 Swap sides so that all variable terms are on the left hand side Swap sides so that all variable terms are on the left hand side 3x9=y 3 x 9 = y Subtract 9 from both sides Subtract 9 from both sides Solve each of the following systems of equations by the method, 2/x 3/y =13; Students can also refer to NCERT Solutions for Class 9 Maths Chapter 4 Linear Equations for Two Variables for better exam preparation and score more marks Linear Equations for Two Variables Class 9 MCQs Questions with Answers Question 1 The value of y at x = 1 in the equation 5y = 2 is (a) \(\frac{5}{2}\) (b) \(\frac{2}{5}\) (c) 10 (d) 0 Answer
If x = 2, y = 1 is a solution by the equation 2x 3y = k, then these value will satisfy the equation ∴ 2 x 23 x 1 = k ⇒ k=43=7 We hope the NCERT Solutions for Class 9 Maths Chapter 4 Linear Equations in Two Variables Ex 42 help you`= x = 42/3 = 14` Hence, the solution of thee given system of equations is x = 14, y = 9 Concept Algebraic Methods of Solving a Pair of Linear Equations Substitution Method RD Sharma Class 9 Solutions Question3 Express x/4 – 3y = – 7 in the form of ax by c = 0 CBSE156DWMW5A Solution Question 4 Find the value of k for which x = 0, y — 8 is a solution of 3x – 6y = k CBSE15NS72LP7 Solution Question 5 Cost of a pen is two and half times the cost of a pencil
If x = a, y = b is the solution of the pair of equation xy = 2 and xy = 4 then what will be value of a and b (a) 2,1 (b) 3,1 (c) 4,6 (d) 1,2 Answer Answer (b) 3,1 If you have any other queries regarding CBSE Class 9 Maths Linear Equations for Two Variables MCQs Multiple Choice Questions with Answers, feel free to reach us via the Answer The graph is a line parallel to xaxis at a distance of 3 from origin Question 7 The cost of a ribbon is twice the cost of a hair pin Write this statement in two variables in linear equation Answer x = 2y, where x is the cost of a ribbon and y is the cost of a hairpin Question 8 Class 9 Maths Formulas By Chapters Chapter 2 – Polynomials Chapter 3 – Coordinate Geometry Chapter 7 – Triangles Chapter 8 – Quadrilaterals Chapter 9 – Areas of Parallelograms and Triangles Chapter 10 – Circles Chapter 12 – Heron's Formula Chapter 13 – Surface Areas and Volumes
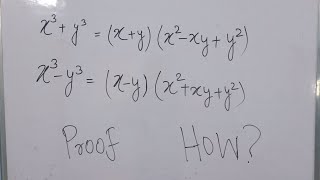



X 3 Y 3 X 3 Y 3 Formula Proof Youtube




Set Formulas Learn Formula For Set In Math
Putting x = 3 and y = 4, we have, 3 × 4 = a × 3 7 ⇒ 12 = 3a 7 ⇒ 12 – 7 = 3a ⇒ a = 5/3 The taxi fare in a city is as follows For the first kilometre, the fare is ₹ 8 and for the subsequent distance it is ₹ 5 per km Taking the distance covered as x km and total fare as ₹ y, write a linear equation for this information MCQs from CBSE Class 9 Maths Chapter 4 Linear Equations in Two Variables 1 The linear equation 3x11y=10 has a) Unique solution b) Two solutions c) Infinitely many solutions d) No solutions Answer/Explanation Answer (c) Explanation 3x11y=10 y=(103x)/11 Now for infinite values of x, y will also have the infinite solutions 0 x y = 3 Which is a linear equation in the variables x and y This is represented by a line Now, all the values of x are permissible because 0x is always 0 However, y must satisfy the equation y = 3 Note that, the graph AB is a line parallel to the xaxis and at a distance of 3 units of the upper side of it Ex 44 Class 9 Maths Question 2




Ex 4 3 5 From The Choices Given Below Choose Equation



Draw The Graph Of Each Of The Following Linear Equations Class 9 Maths Cbse
Linear Equations In Two Variables Notes For Class 9 Formulas Download PDF LINEAR EQUATION IN TWO VARIABLES An equation of the form ax by c = 0 where a, b, c are real numbers and x, y are variables, is called a linear equation in two variablesClick here👆to get an answer to your question ️ The equation y^2e^xy = 9e^3x^2 defines y as a differentiable function of x The value of dy/dx for x = 1 and y = 3 is5/x 4/y = 2 where x ≠ 0 and y ≠ 0 asked in Mathematics by sforrest072 ( 128k points) pair of linear equations in two variables
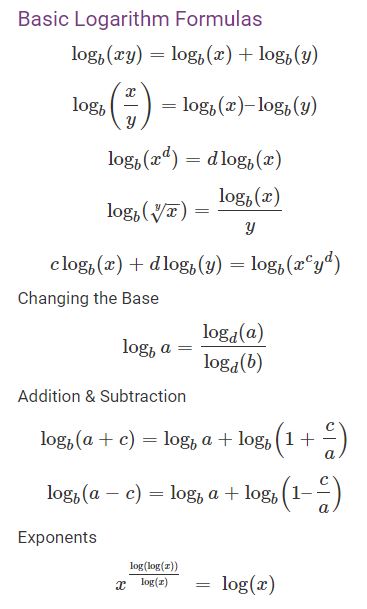



Logarithms Rs Aggarwal Icse Class 9th Maths Goyal Brothers Prakashan Icsehelp




Notes Of Ch 2 Polynomials Class 9th Math
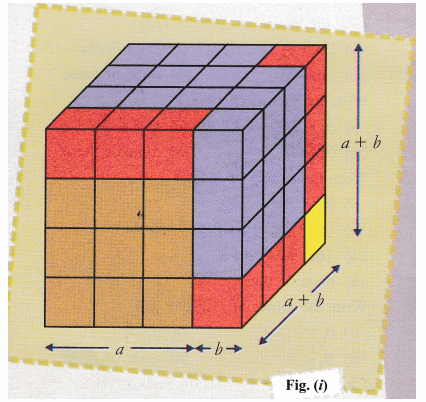
The algebraic formulas for the three variables a, b and c and a maximum degree of 3 can be quickly taken by multiplying the expression by itself, based on the exponent value of the algebraic expression You can see the basic algebraic formulas given below 1 (a b)2 = a2 2ab b2 2 (a– b)2 = a2– 2ab b2Answer (1) In one variable, 2 x 9 = 0 represents a point as shown in the following figure (2) In two variables, 2 x 9 = 0 represents a straight line passing through point (−45, 0) and parallel to y axis It is a collection of all points of the plane, having their x coordinate as 45Algebraic identities chapter is introduced in CBSE class 9 This is a tricky chapter where one needs to learn all the formula and apply them accordingly To make it easy for them, BYJU'S provide all the formulas on a single page We believe, algebra formulas for class 9 will help students to score better marks in mathematics




Maths Formulas For Class 9 Learn Cram




Ncert Solutions Class 9 Maths Chapter 4 Linear Equations In Two Variables
Step 2 Express y in terms of x ie y = ((ax b)/c)) Step 3 Put any two or three values for x and calculate the corresponding values of y from the expression values of y from the expression obtained in step 2 Let we get points as (α1, β1), (α2, β2), (α3, β3) Step 4 Plot points (α1, β1), (α2, β2), (α3, β3) on graph paperII The x and ycoordinates of a point is the perpendicular distance from the Yaxis and Xaxis measured along the X and Yaxes respectively III The ycoordinate of any point Xaxis is zero and xcoordinate of any point on Yaxis is zero IV The axes divides the plane into four quadrants 1 In 1st quadrants x > 0, y > 0 ie (, ) 2 Since there are infinite lines passing through the point (2, 3) Let, first equation is x y = 5 and second equation is 2x 3y = 13 Clearly, the lines represented by both equations intersect at the point (2, 3) Question 4 If ax 3y = 25, write y in terms of x and also, find the two solutions of this equation Solution Question 5




Http Www Aplustopper Com Solving A Quadratic Equation By Factoring Quadratics Quadratic Equation Maths Solutions




Algebra Formulas For Class 9 Pdf Download Free Here
In addition, we also provided basic maths formulas for Classes 12, 11, 10, 9, 8 which are used in our day to day lives to calculate the space, length and so on Geometry Formulas for Class 8 to 12 PDF Download Main Concern of every student about the subject is to learn about Geometry Formulas There are some basic formulas that you really need Algebraic Identities For Class 9 (ab)2 = a2 2abb2 ( a b) 2 = a 2 2 a b b 2 (a−b)2 = a2 −2abb2 ( a − b) 2 = a 2 − 2 a b b 2 (ab)(a–b) = a2 –b2 ( a b) ( a – b) = a 2 – b 2 (xa)(xb) =x2 (ab)xab ( x a) ( x b) = x 2 ( a b) x a bFree PDF download of NCERT Solutions for Class 9 Maths Chapter 4 Exercise 43 (Ex 43) and all chapter exercises at one place prepared by expert teacher as per NCERT (CBSE) books guidelines To get the copy of latest Class 9th Maths Chapter 4 Exercise 43




X Y 3 X 3 Y 2 6 Youtube



Cbse Class 9 Maths Lab Manual Algebraic Identity A B 3 A3 3a2b 3ab2 Cbse Sample Papers
Ex 63, 8 Solve the following system of inequalities graphically x y ≤ 9, y > x, x ≥ 0 First we solve x y ≤ 9 Lets first draw graph of x y = 9 Putting x = 0 in (1) 0 y = 9 y = 9 Putting y = 0 in (1) x 0 = 9 x = 9 Points to be plotted are (0, 9), (9, 0) Drawing graph Checking for (0,0) Putting x = 0, y = 0 x y ≤ 9 0 0 ≤ 9 0 ≤ 9 which is true Hence origin lies in plane x y ≤ 9 So, we shade left side of line Now we solve y > x Lets first draw graph of y = xLinear Equations in two variablesTest 1 Show that x = 2 and y = 1 satisfy the linear equation 2x 3y = 7 2 Write four solutions of 2x 3y = 8 3 Draw the graph of the equation 2x – 3y = 12P yare quadratic surds and if a p x= b p ythen a= band x= y 23 If a;m;nare positivereal numbersanda6=1,thenlog a mn=log a mlog a n 24 If a;m;nare positive real numbers, a6=1,thenlog a m n =log a m−log a n 25 If aand mare positive real numbers, a6=1thenlog a mn




Maths Formulas For Class 9 Cbse Important Maths Formulas




Exercise 2e Of Rs Aggarwal Class 9 Maths Solutions Chapter 2 Polynomials
This is obtained from the binomial theorem by setting x = 1 and y = 1 The formula also has a natural combinatorial interpretation the left side sums the number of subsets of {1, , n} of sizes k = 0, 1, , n, giving the total number of subsets (That is, the left side counts the power set of {1, , nSolution For The equation x^(3)x^(2)yxy^(2)=y^(3) represents Become a Tutor Blog Cbse Question Bank Pdfs Micro Class Download App Class 12 Math Coordinate Geometry Pair Of Straight Lines 504 150 The equation x 3 x 2 y − x y 2 = y 3 NCERT Solutions for Class 9 Maths Chapter 8 Linear Equations in Two Variables Ex Question 1 Draw the graph of each of the following linear equations in two variables (i) x y = 4 (ii) x – y = 2 (iii) y = 3x (iv) 3 = 2x y




R D Sharma Solutions Class 9th Ch 13 Linear Equations In Two Variables Exercise 13 3




Ncert Solutions For Class 9 Maths Chapter 6 Lines And Angles
Let the contributions of Yamini and Fatima be Rs x and Rs y respectively Then according to the question x y = 100 This is the linear equation which the given data satisfies Now, x y = 100 ⇒ y = 100 – x Table of solutions RS Aggarwal and Veena Aggarwal Class 9 Chapter 4 (Linear Equations in Two variables) Exercise 4A Solution Go main page of RS Aggarwal Class 9 Solution Question 1 Express each of the following equations in the form axbyc=0 and indicate the values of a, b, c in each case (i) 3x5y=75 ⇒3x5y=15/2 ⇒6x10y15= 0 Multiplying by 2 both sideCBSE NCERT Notes Class 9 Maths Polynomials Show Topics Class 9 Maths Polynomials Algebraic Identities Algebraic Identities Algebraic identity is an algebraic equation that is true for all values of the variables occurring in it ( x y) 2 = x2 2 xy y2 ( x – y) 2 = x2 – 2 xy y2 x2 – y2 = ( x y) ( x – y)




Algebraic Identities Of Polynomials A Plus Topper




Ncert Solutions For Class 9 Maths Chapter 2 Polynomials Ex 2 5 Cbsetuts Com
Solve the equations using matrix method 3x y 2z = 3, 2x – 3y – z = 3 x 2y z = 4 asked in Matrices by Mohini01 ( 677k points) matricesBiquadratic Polynomial = \( x^4 5x^3 2x^2 3 \) Class 9 Coordinate Geometry Formulas Equation of a line = \( ax by c = 0 \) Equation of a circle = \( x^2 y^2 = r^2 \) Here 'r' is the radius of the circle; Ex 93, 1Form a differential equation representing the given family of curves by eliminating arbitrary constants and =1 Here , we Eliminate Constant by Differentiating both sides wrtx =1Differentiating Both Sides wrt 1 1 =0 1




Verify I X 3 Y 3 X Y X 2 X Y Y 2 Ii X 3 Y 3 X Y X 2 X Y Y 2




Cbse Class 9 Maths Chapter 5 Introduction To Euclids Geometry Formulas Geometry Formulas Euclid Geometry Math
Equation of a parabola = \( y^2 = 4ax \) Equation of an ellipse = \( \frac{{x^2 }}{{a^2 }} \frac{{y^2 }}{{b^2 }} = 1 \) 9th Class Formulas For Algebraic Identities Given below are the algebraic identities which are considered very important maths formulas for Class 9 (a b) 2 = a 2 2ab b 2 (a – b) 2 = a 2 – 2ab b 2 (a b) (a – b) = a 2 b 2 (x a) (x b) = x 2 (a b) x ab (x a) (x – b) = x 2 (a – b) x – ab 3 A threewheeler scooter charges Rs 15 for first kilometer and Rs 8 each for every subsequent kilometer For a distance of x km, an amount of Rs y is paid Write the linear equation representing the above information Solution Total fare of Rs y for covering the distance of x km is given by y = 15 8(x − 1) y = 15 8x − 8 y = 8x 7
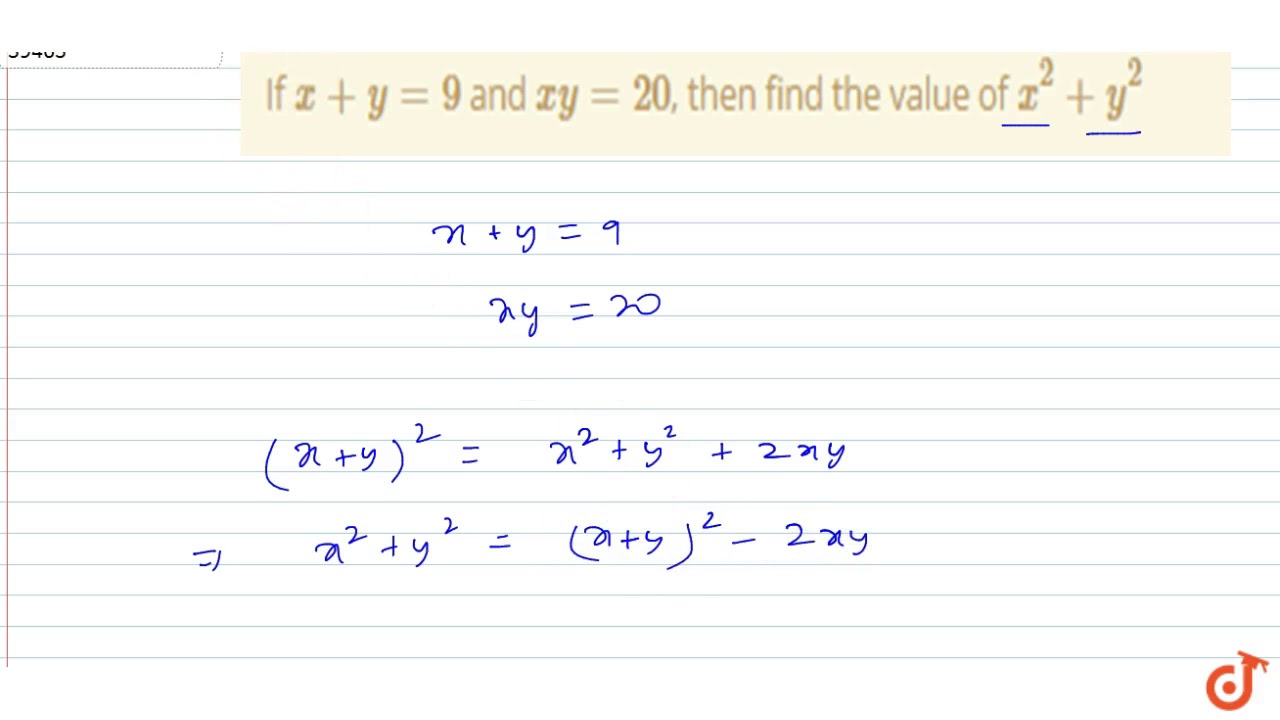



If X Y 9 And Xy Then Find The Value Of X 2 Y 2 Youtube



1
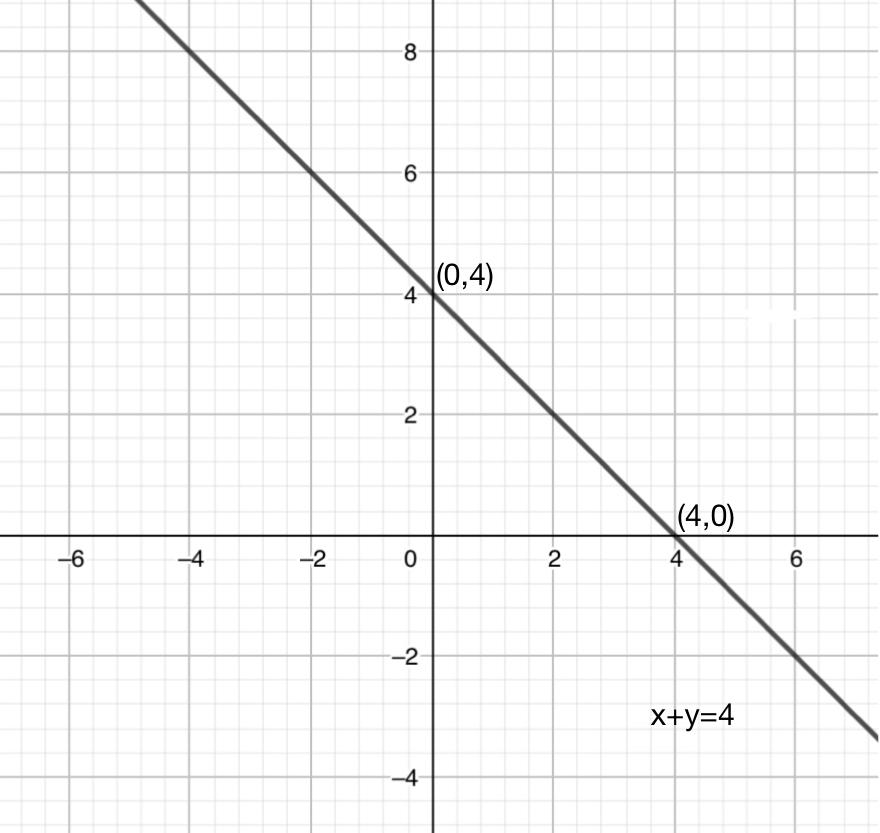
Exercise 43 Question 1 Draw the graph of each of the following linear equation in two variables y = 4 – 0 = 4 So the solution is (0, 4) y = 4 – 1 = 3 So the solution is (1, 3) y = 4 – 2 = 2 So the solution is (2, 2) x = 2 0 = 2Selina solutions for Concise Mathematics Class 9 ICSE chapter 6 (Simultaneous (Linear) Equations (Including Problems)) include all questions with solution and detail explanation This will clear students doubts about any question and improve application skills while preparing for board exams The detailed, stepbystep solutions will help you understand the concepts better and clear your Solve all the important problems and questions in Maths with the Best Maths Formulas for Class 9 Maths Formulas for Class 9 PDF Free Download Feel free to directly use the best Maths formulas during your homework or exam preparation You need to know the list of Class 9 formulas as they will not just be useful in your academic books but also in your day to day lives Remember the Maths Formulas




上 X Y 5 X2 Y25 シモネタ




Ex 2 5 12 Verify That X3 Y3 Z3 3xyz 1 2 Ex 2 5
9th Class Formulas For Algebraic Identities Given below are the algebraic identities which are considered very important maths formulas for Class 9 (a b) 2 = a 2 2ab b 2 (a – b) 2 = a 2 – 2ab b 2 (a b) (a – b) = a 2 b 2 (x a) (x b) = x 2 (a b) x ab (x a) (x – b) = x 2 (a – b) xP yare quadratic surds and if a p x= p y,thena= 0 and x= y 22 If p x;Answer satisfying (1,3) in 3x4y9=0 ⇒ 3×1−4×39 = 0 ⇒ 3−129= 0 ⇒ 12−12= 0 ⇒ 0= 0 ∴ LHS=RHS Hence proved Answer verified by Toppr Upvote (0)



Cbse 9 Math Cbse Linear Equations In Two Variables Ncert Solutions




Important Questions Class 9 Maths Chapter 2 Polynomial Part 1 Polynomials Maths Formula Book Writing Linear Equations
Give the geometric representations of y = 3 as an equation (i) in one variable (ii) in two variables Solution (i) y = 3 ∵ y = 3 is an equation in one variable, ie, y only ∴ y = 3 is a unique solution on the number line as shown below (ii) y = 3 We can write y = 3 in two variables as 0x y = 3 Now, when x = 1, y = 3 x = 2, y = 3 x = 1, y = 3Class IX MathSample Paper For Linear Equations in Two Variables 1 Show that x = 1, y = 3 satisfy the linear equation 3x – 4y 9 = 0 2 Look at the following graphical representation of an equation Which of the points (0, 0) (0, 4) or (– 1, 4) is a solution of the equation?




Ex 3 3 1 I Solve By Substitution X Y 14 X Y 4 Video




Telangana Scert Class 9 Math Solution Chapter 12 Circles Exercise 12 3



Class 9 Math Formula List And Tables




Cbse Class 9 Maths Chapter 3 Coordinate Geometry Formulas
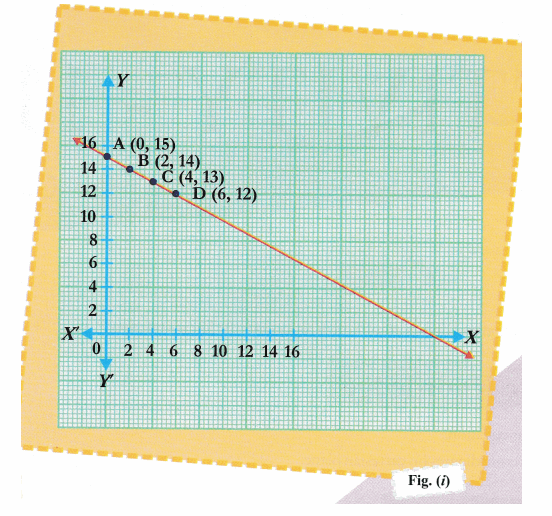



Cbse Class 9 Maths Lab Manual Graph Of Linear Equation Cbse Sample Papers




Ncert Solutions For Class 9 Maths Chapter 2 Exercise 2 5 Polynomials




Ncert Solutions For Class 9 Maths Chapter 2 Polynomials




X Y 3 Y Z 3 Z X 3 3 X Y Y Z Z X 2 X3 Y3 Z3 3xyz Mathematics Topperlearning Com T86qex55




Kerala Syllabus 9th Standard Maths Solutions Chapter 3 Pairs Of Equations Hsslive




Ncert Solutions For Class 9 Maths Chapter 6 Lines And Angles Exercise 6 1



26 Free Simultaneous Equations Worksheets And Lesson Plans For Ks3 And Ks4 Maths




If X Y Z 0 Show That X 3 Y 3 Z 3 3xyz With Video




Class 9 Geometry Pdf




Ncert Solutions Class 9 Maths Chapter 2 Exercise 2 4 Polynomials




Selina Solutions Class 9 Concise Maths Chapter 5 Factorisation Download Free Pdf
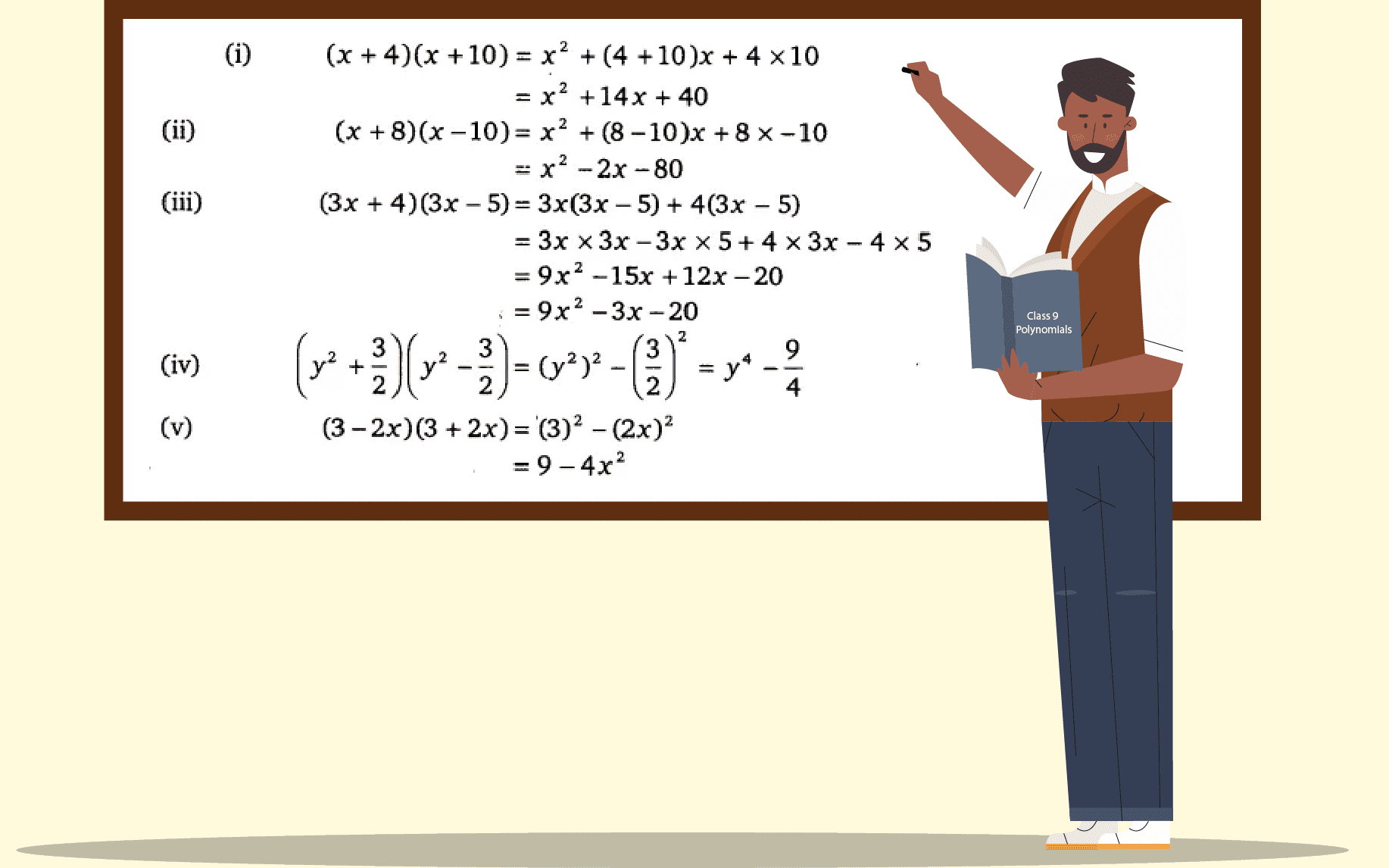



How To Solve Bodmas Questions Rules Worksheets Leverage Edu
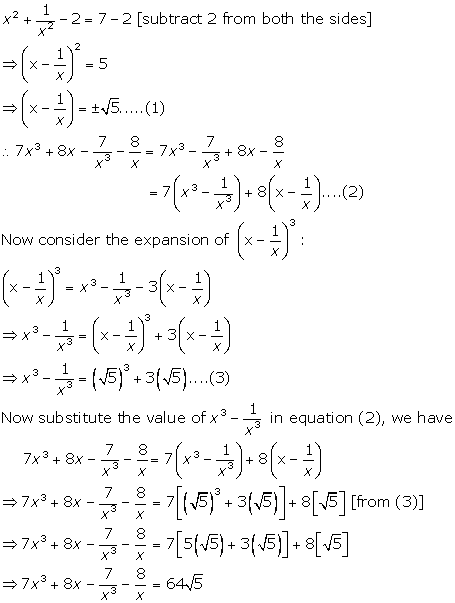



Chapter 4 Expansion Selina Concise Mathematics Part I Solutions For Class 9 Mathematics Icse Topperlearning




Standard Identities Of Binomials And Trinomials Equations Examples




Ex 3 3 2 Plot The Point X Y Given In The Following
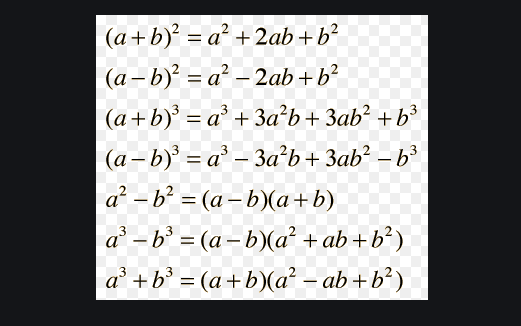



Expansions Ml Aggarwal Icse Class 9 Maths Solutions Icsehelp
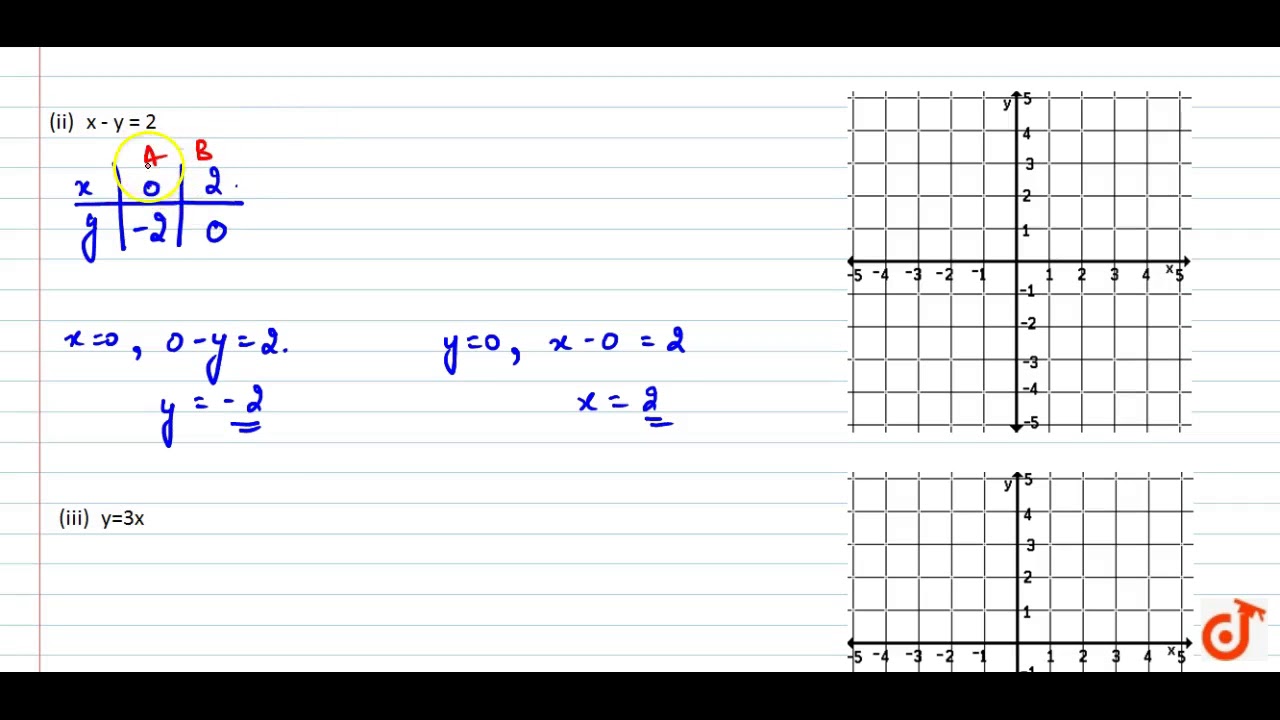



Draw The Graph Of Each Of The Following Linear Equations In Two Variables I X Y 4 Ii X Y Youtube




X 3 Y 3 X 3 Y 3 Formula Proof Youtube



1




Verify X3 Y3 And X3 Y3 Std 9 Maths Ex 2 5 Q 9 Youtube




Ex 2 5 11 Factorise 27 X3 Y3 Z3 9xyz Class 9 Ex 2 5




X Y 6 X Y 4 Practice Set 1 2 Simultaneous Equation Graphically Graph Method Grade 10 Youtube
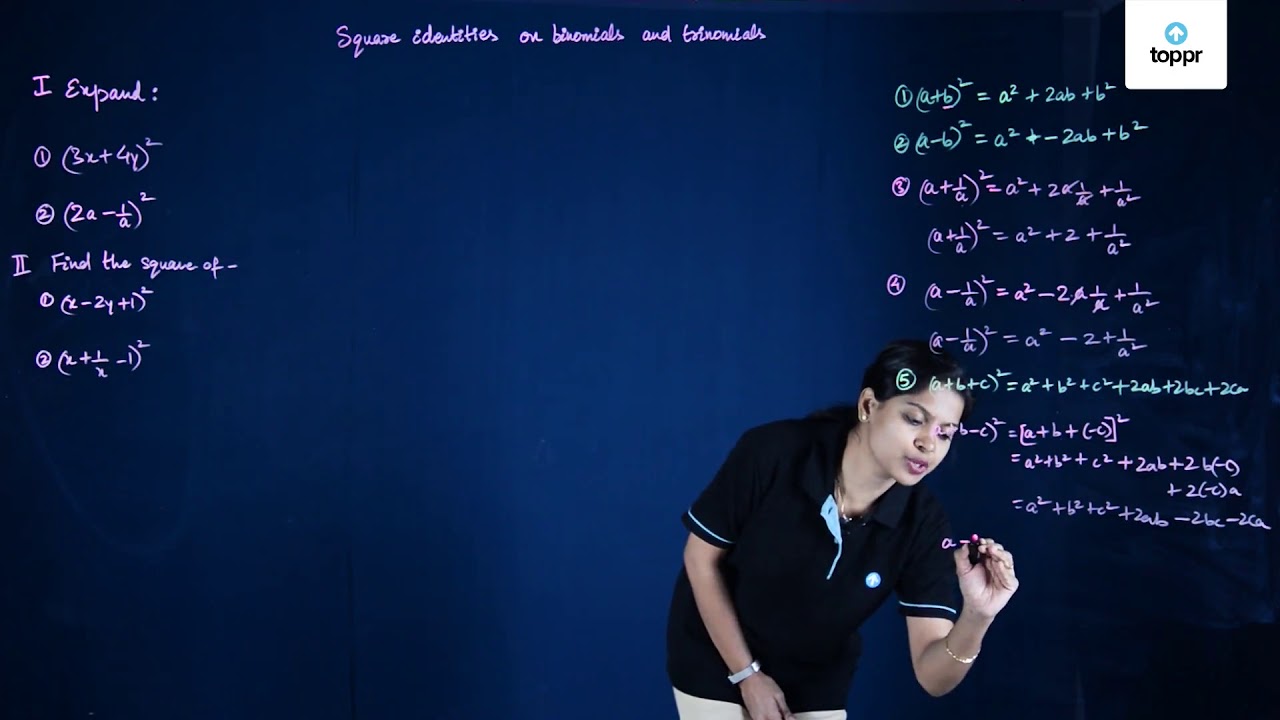



Standard Identities Of Binomials And Trinomials Equations Examples




Important Maths Formulas For Class 6 7 8 9 10 11 12 Cbse Board Version Weekly




Factorisation Worksheet Class 9 Printable Worksheets Are A Precious Lecture Room Tool They In 21 Math Addition Worksheets Algebra Equations Worksheets Mathematics
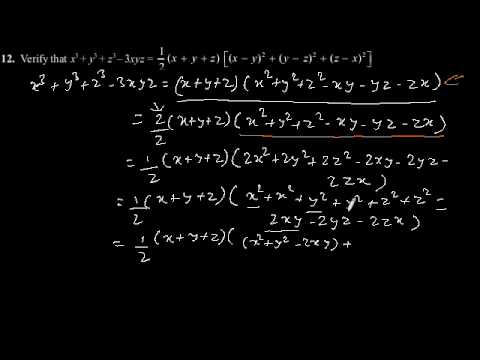



Cbse Class 9 Maths Ncert Solution Polynomial Exercise 2 5 Problem 12 Youtube




Ncert Solutions Class 9 Maths Chapter 2 Exercise 2 4 Polynomials




Simplify X Y 3 X Y 3 6y X 2 Y 2 Youtube




Which Of The Pairs Of Linear Equations Has Unique Solution No Solution




Verify That X3 Y3 Z3 3xyz 1 2 X Y Z X Y 2 Y Z 2 Z X 2 Class 9th Ex 2 5 Question 12 Youtube




Mathematics Class 9th Chapter 4 Solution



1



Uwutfuihwfilam




If X Y 9 X Y 14 Then Find X Y Youtube




Ncert Solutions For Class 9 Herons Formula




Ncert Solutions For Class 9 Maths Chapter 4 Linear Equations In Two Variables




For What Value Of N Is Following A Homogeneous Differential Equation




Ncert Solutions For Class 9 Maths Chapter 4 Linear Equations In Two Variables




Ncert Solutions For Class 9 Maths Chapter 6 Lines And Angles




Cbse Class 9 Heron S Formula For Class Ix By Unacademy
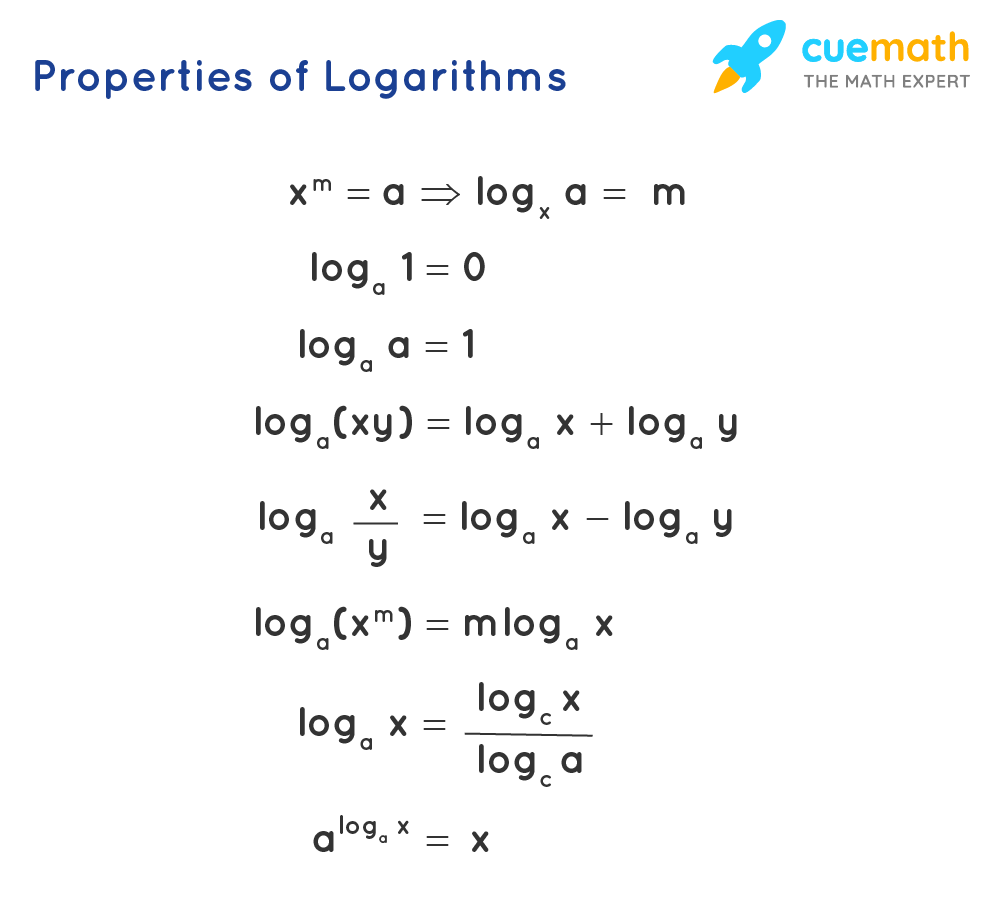



Algebra Formula Solved Examples List Of Algebraic Formulas




Example 7 Find Coefficient Of X6y3 In Expansion X 2y 9




Ncert Solutions Class 9 Maths Chapter 4 Linear Equations In Two Variables
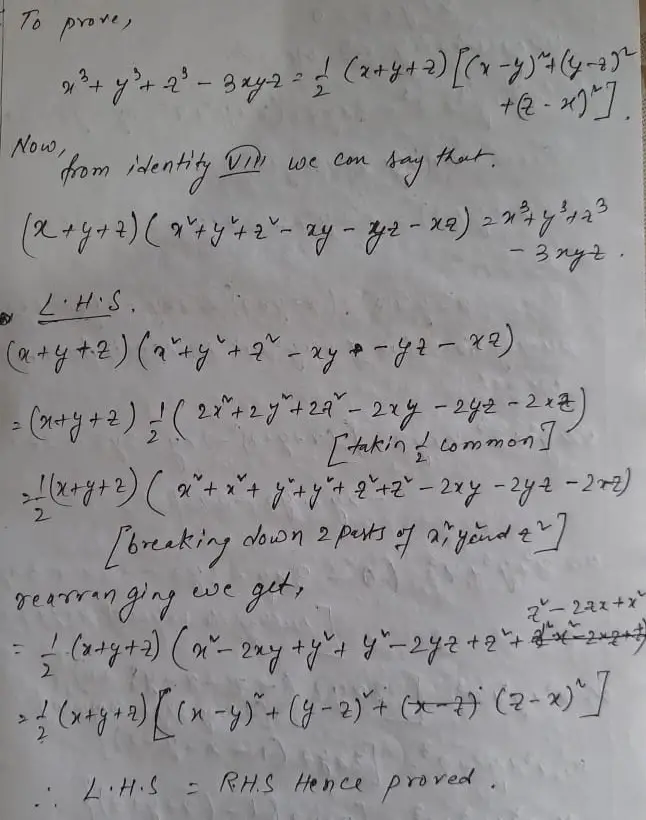



Telangana Scert Class 9 Math Solution Chapter 2 Polynomials And Factorisation Exercise 2 5




Gseb Solutions For Class 9 Mathematics Linear Equations In Two Variables Cbse Tuts




Example 6 Draw The Graph Of X Y 7 Chapter 4 Examples




Solve The Following System Of Equations 27 X Y 15 X Y 2 And 30 X Y 1 X Y 3 Mathematics Topperlearning Com X68shsoo




Ncert Solutions For Class 9 Maths Chapter 4 Linear Equations In Two Variables




Ncert Solutions For Class 9 Maths Chapter 4 Linear Equations In Pdf




Algebraic Identities Of Polynomials A Plus Topper




Rd Sharma Class 9 Chapter 4 Algebraic Identities Updated For 21 22




Chapter 4 Expansion Selina Concise Mathematics Part I Solutions For Class 9 Mathematics Icse Topperlearning




R D Sharma Solutions Class 9th Ch 13 Linear Equations In Two Variables Exercise 13 3




Ex 2 5 9 Verify I X 3 Y 3 X Y X 2 Xy Y 2 Teachoo




Kerala Syllabus 9th Standard Maths Solutions Chapter 3 Pairs Of Equations Forms In Malayalam Hsslive




Simplify X Y 3 X Y 3 6y X 2 Y 2




Solve 2xy X Y 3 2 Xy 2x Y 3 10 Mathematics Topperlearning Com X2oivz99




Maths Formulas For Class 6 7 8 9 10 11 And 12 Pdf Download Version Weekly




Ex 3 2 7 I Class 12 Matrices Find X And Y If X Y And X
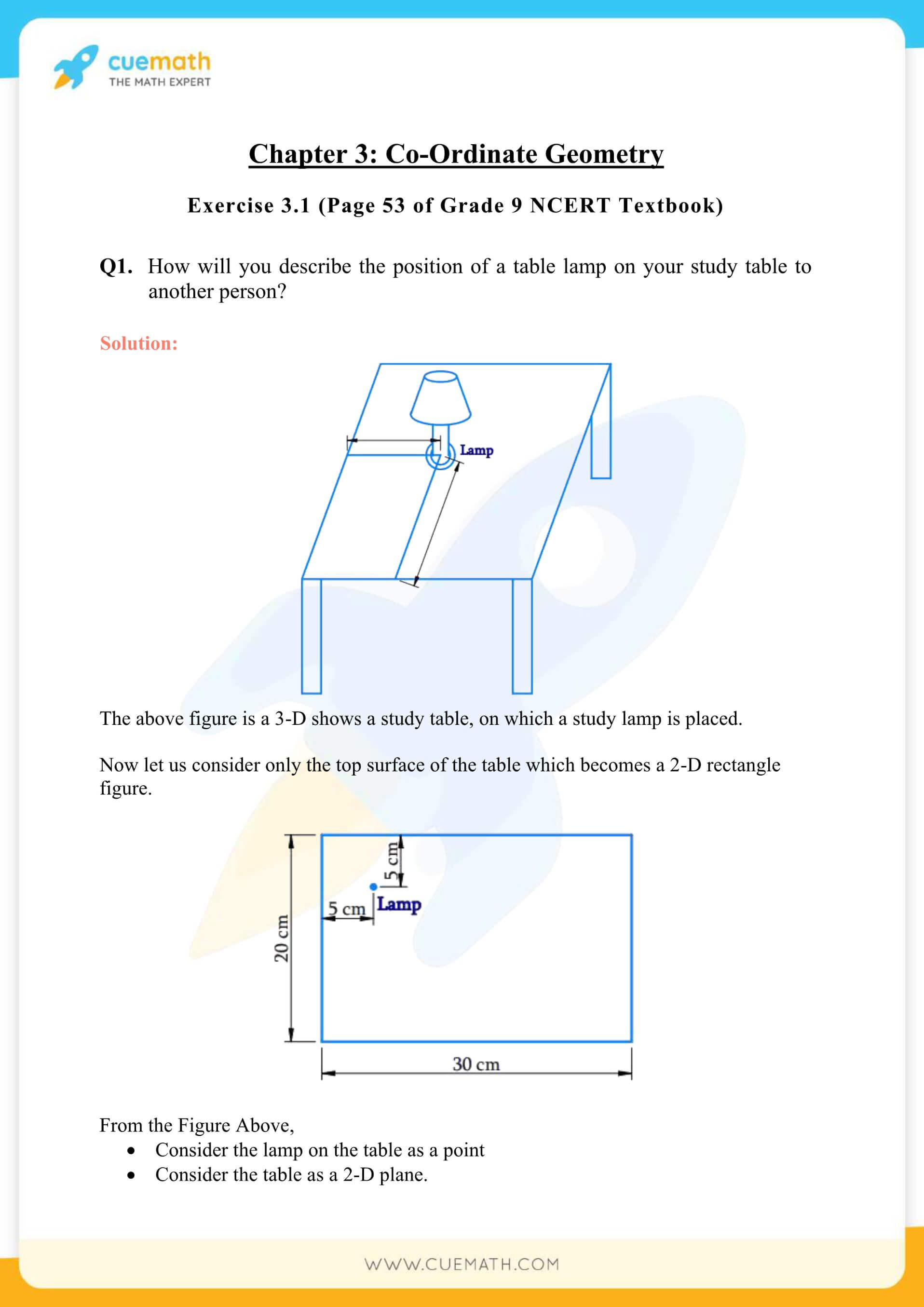



Ncert Solutions Class 9 Maths Chapter 3 Exercise 3 1 Coordinate Geometry




Ncert Solutions For Class 9 Maths Chapter 4 Linear Equations In Pdf




Ncert Solutions For Class 9 Maths Chapter 4 Linear Equations In Two Variables Ex 4 3 Cbsetuts Com
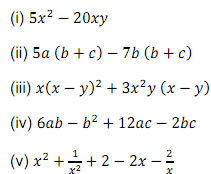



Maths Formulas For Class 9 Cbse Chapter 3 Coordinate Geometry



Polynomials Class 9th Formula Studyrankersonline




Rd Sharma Class 9 Solutions Chapter 4 Algebraic Identities




X 2 2y 3 1 And X Y 3 3 Find X And Y Values Using Elimination And Substitution Method Youtube



If X Y 12 And Xy 27 Then Find The Value Of X3 Y3 Polynomials Maths Class 9




Polynomials Class 9 Notes Maths Chapter 2 Learn Cbse




The Value Of X Y 3 Y Z 3 Z X 3 9 X Y Y Z Z X Is Equal To A 0 B 1 9 C 1 3 D 1




Graphing A Linear Equation Y 2x 7 Video Khan Academy




Algebra Formulas For Class 9 Pdf Download Free Here




Factorization Of Cubic Polynomials Important Questions Class 9 Polynomials Class 9 Ex 2 5 Q9 Youtube




Maharashtra Board Class 9 Maths Solutions Chapter 4 Ratio And Proportion Practice Set 4 4 Learn Cram



1



0 件のコメント:
コメントを投稿